Summary Of Data Structure

Preface
Summarize what I learned from the data structure class and some of its implementation in different language.

Category

• Array
• LinkedList
• Stack
• Queue
• Heap
• Map
  • HashMap/Dictionary
  • LinkedHashMap/OrderedDict
• Tree
  1. Binary Search Tree
  2. B tree
     • B-tree
     • B+tree
     • B* tree
  3. Red-Black Tree
• Graph
  • Quick Find
  • Quick Union
  • Weighted Quick Union
  • Path Compression
  • Weighted + Path

Array

Structure

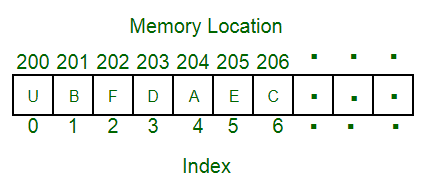
Member Function Time Complexity

Action	Worst Time Complexity
Add	O(1)
Access By Index	O(1)
Search	O(N)
Insert	O(N)
Resize	O(N)
Delete	O(N)

Implementation in different language

C++

1. Array—Fixed Size In Stack
   Example:

   #include <iostream>
   using namespace std;
   
   int main(){
       int arr[]={10,20,40,60};
       int *p=arr;
       cout<<arr<<endl;
       cout<<arr+1<<endl;
       cout<<*p<<endl;
       cout<<*(p+2)<<endl;
       cout<<p[3]<<endl;
       cout<<&p<<endl;
       return 0;
   }

2. Dynamic Array–Can Change Size During Runtime

int* a = NULL;   // Pointer to int, initialize to nothing.
int n;           // Size needed for array
cin >> n;        // Read in the size
a = new int[n];  // Allocate n ints and save ptr in a.
for (int i=0; i<n; i++) {
    a[i] = 0;    // Initialize all elements to zero.
}

delete [] a;  // When done, free memory pointed to by a.
a = NULL;     // Clear a to prevent using invalid memory reference.

Java

1. Plain Array
   Much Similar As what is done in C++
2. ArrayList(Defined in JDK library)

Def: An Object Class that implements List Interface
Note that ArrayList used static function of Arrays to do the resize

public static <T,U> T[] copyOf(U[] original, int newLength, Class<? extends T[]> newType)
{
 @SuppressWarnings("unchecked")
 T[] copy = ((Object)newType == (Object)Object[].class)
            ? (T[]) new Object[newLength]
            : (T[]) Array.newInstance(newType.getComponentType(), newLength);
System.arraycopy(original, 0, copy, 0,
                         Math.min(original.length, newLength));
return copy;
}

1. The Java Virtual Machine used reflection mechanism to initialize a new Array object with the new size during runtime
2. Copy the old element to the new Array

Python

In python, one can use list to serve as an array

Linked List

Structure

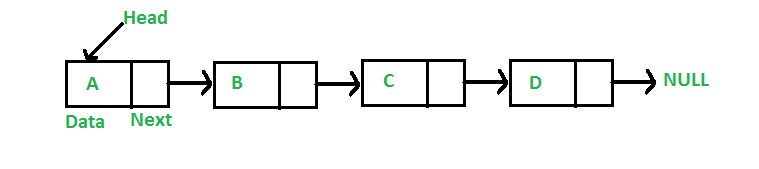
Member Function Time Complexity

Action	Worst Time Complexity
Add	O(1)
Access By Index	O(N)
Search	O(N)
Insert	O(N)
Resize	O(1)
Delete	O(N)

Implementation in different language

C++

Example:

#include <iostream>

using namespace std;

struct node
{
    int data;
    node *next;
};

class linked_list
{
private:
    node *head,*tail;
public:
    linked_list()
    {
        head = NULL;
        tail = NULL;
    }

    void add_node(int n)
    {
        node *tmp = new node;
        tmp->data = n;
        tmp->next = NULL;

        if(head == NULL)
        {
            head = tmp;
            tail = tmp;
        }
        else
        {
            tail->next = tmp;
            tail = tail->next;
        }
    }
};

Java

Predefined LinkedList that implements List interface

Python

Def Node

class Node(object):

    def __init__(self, data=None, next_node=None):
        self.data = data
        self.next_node = next_node

    def get_data(self):
        return self.data

    def get_next(self):
        return self.next_node

    def set_next(self, new_next):
        self.next_node = new_next

Def linkedList

class LinkedList(object):
    def __init__(self, head=None):
        self.head = head

    #...omitted#

Stack

FILO: First In Last Out

Structure

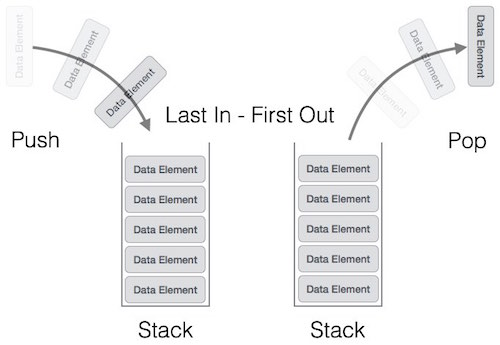
Member Function Time Complexity

Action	Worst Time Complexity
Push	O(1)
Pop	O(1)

Implementation in Different Language

C++

#ifndef STACK_H
#define STACK_H
#include <cstdlib>
#include "node.h"
using namespace std;


template <class T>
class stack{
 public:
  // constructor
  stack();

  // modifiers
  void push(T entry);
  void pop();

  // accessors
  bool empty();
  T top();
 private:
  node<T>* head;
};
#include "stack.cpp"
#endif

Java

Can use ArrayList to serve as Stack

Python

Can use list

Queue

FIFO:First In Last Out

Structure

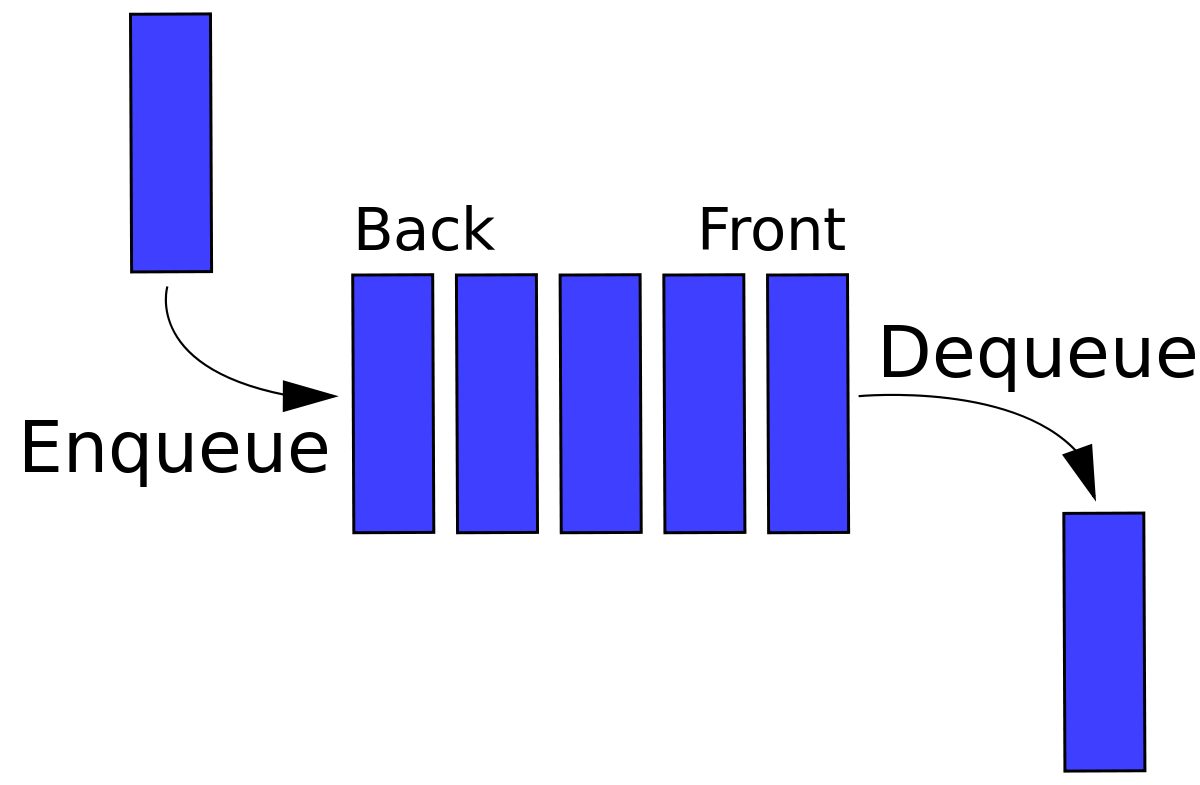
Heap

• MinHeap
• MaxHeap
  Can be implemented using Array

Time Complexity

Action	Worst Time Complexity	Step
insert	O(logN)	NA
delete min	O(logN)	Switch min with the last entry and heapify
Sort	O(NlogN)	build a min heap, delete min iteratively

Map

Structure

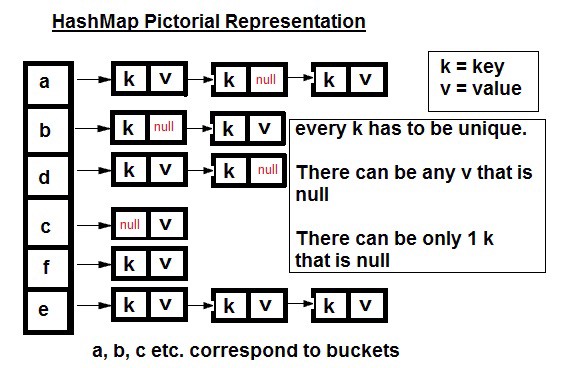
Hashing

• Probing
  • Linear Probing: When Collision happens, always find the nex spot
  • Quadratic Probing: When Collision happens, always find the next i^2 spots
• Chained Hashing
  • When collision happens, Link the same hash element

Implementation

1. Python
   • Dict
   • OrderedDict
2. Java
   • HashMap
   • LinkedHashMap

Tree

1. Binary Tree
   • Full Binary Tree
   • Complete Binary Tree
   • Consider the Skewed Case

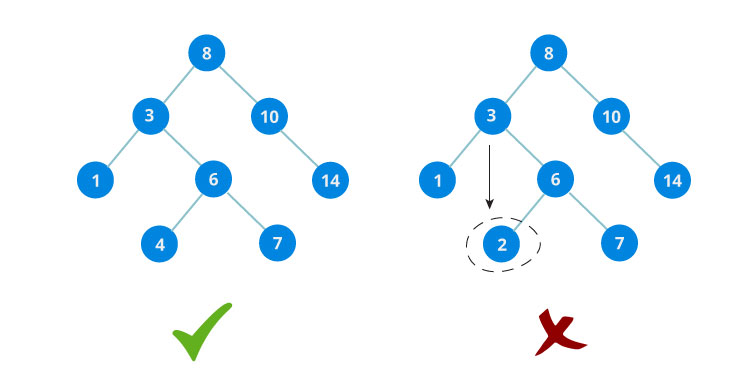
Action	Worst Time Complexity
insert	O(N)
delete	O(N)
search	O(N)

2. B tree（Self Balanced）

Action	Worst Time Complexity
insert	O(logN)
delete	O(logN)
search	O(logN)

Difference Between different B tree

• B-tree: Self Balanced Search Tree

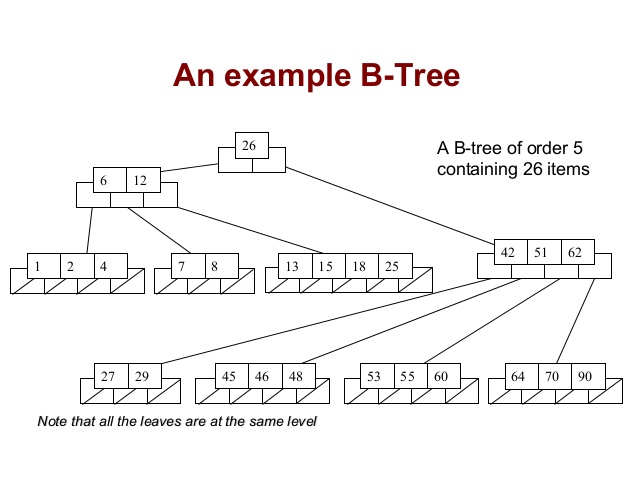
• B+tree: Only the leaf Node store the data, Non-leaf node only contains the key as road map

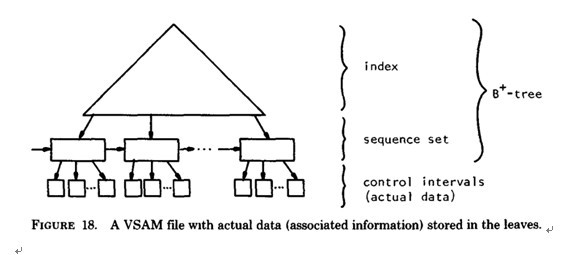
• B* tree: Contains the pointer to brother node

3. Red-Black Tree

• Root of the tree is always black
• No adjacent red node
• Every path from a node to any of its descendent null node has the same number of black node
  

Graph

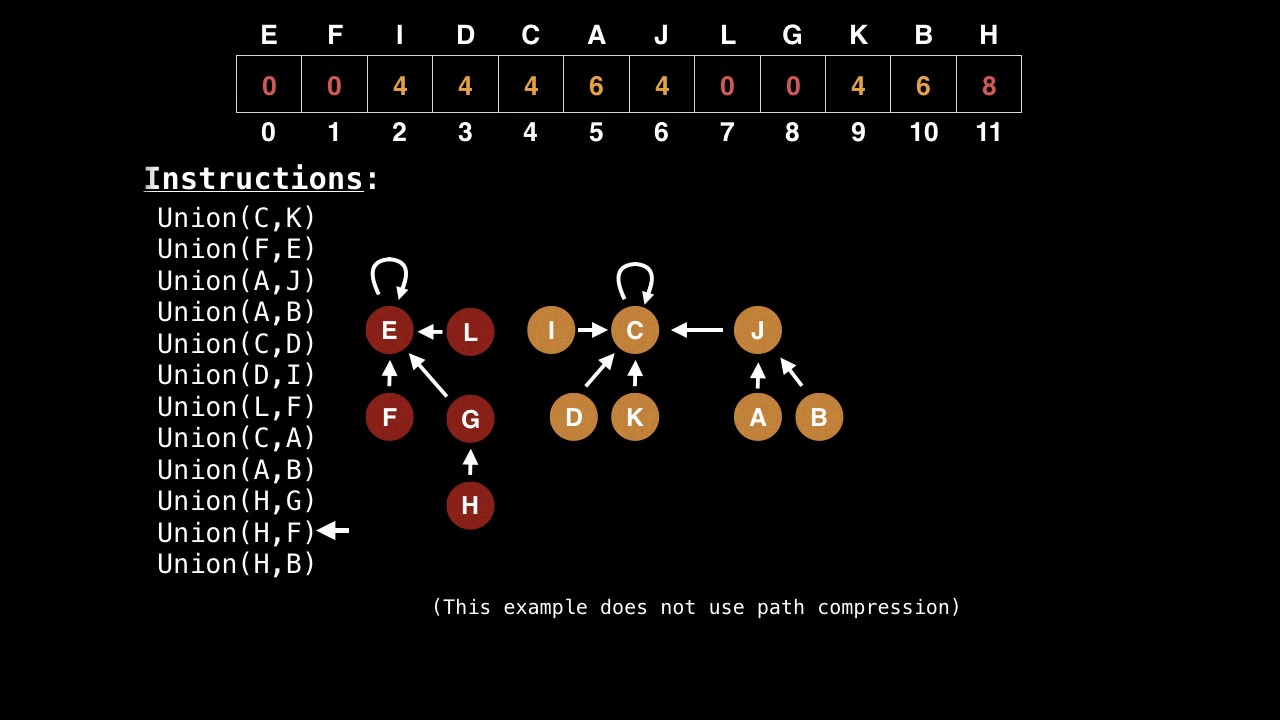
With M union and find Operation on N graph Node objects

Time Complexity

type of union-find	Worst Time Complexity
Quick-find	MN
Quick-union	MN
weighted Union	N+MlogN
Path Compression	N+MlogN
weighted+Path	(M+N)log* N